Current and Past Research Projects

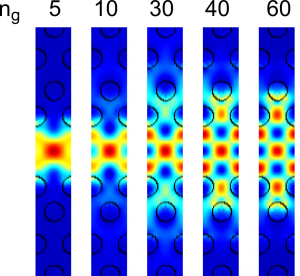
Science fiction fans never stop wondering about the consequences of being able to accelerate massive particles to speeds that exceed the speed of light in vacuum. Of course, this is still just a dream, but recent work has shown that it is possible to slow down the group velocity of light by many orders of magnitude or even find situations in which the group velocity exceeds the speed of light in vacuum. Work performed by other researchers and myself has shown that it is possible to slow light to approximately the same speed as that of an automobile; this slowdown occurs by making use of the strong dispersion of the refractive index that occurs near the resonance frequencies of atomic vapors or certain crystalline solids. Our team is also working on the development of photonic crystal waveguides that can similarly slow the velocity of light. The motivation of this latter approach is that it would allow slow-light methods to be integrated into existing photonic-device platforms, leading to increased functionality for applications such as buffers and routers. Another application under development is the construction of spectrometers that contain slow-light elements. Theoretical arguments show that such a spectrometer could be fabricated in millimeter dimensions on an optical chip, yet nonetheless possess the same spectral resolution as a laboratory (meter-size) spectrometer.

One aspect of our work involves the development of methods for controlling the velocity at which light pulses travel through material systems. Applications of these “slow-light” methods include the development of routers and buffers for optical telecommunications and enhanced nonlinear optical interactions. As a specific example, as part of this program we will develop a chip-scale spectrometer that, by means of slow-light methods, can provide the same spectral resolution as that of large laboratory-scale instruments. This spectrometer will be constructed using nanofabrication methods to create photonic-crystal structures that display strong slow-light effects. Such devices have enormous implications for applications such as medical diagnostics and the detection of terrorism threats. Another aspect of our work entails the development of optical methods for quantum information science. Our approach is motivated by the observation that the transverse degree of freedom of the photon constitutes an extremely large state space. Consequently, large amounts of information can be carried even by a single photon. This large information capacity can be exploited in the context of quantum imaging, for instance to provide superresolution and the transmission of complete images using only a small number of photons. Another application, which will be a primary goal of our research, is to develop a quantum cryptography system in which each photon carries many bits of information. This increased information capacity can increase dramatically the transmission rates of systems for quantum key distribution.

The photonics program at the University of Ottawa, including my CERC Program, has made a major commitment to nanotechnology and specifically to develop a full-range nanofabrication facility within our new photonics building. The facility will contain all of the basic elements of a modern nanofabrication facility, including an e-beam writer, a plasma etching station, mask aligner, and associated diagnostic equipment such as a scanning-electron microscope system, ellipsometer, profilometer, and various wave-guide characterization systems.
This fabrication facility will be crucial to the success of the development of slow-light waveguides and the slow light spectrometer mentioned above. We are also interested in fabricating structured waveguides with properties tailored to enhance the nonlinear optical response, which could lead to highly efficient switching devices. Currently the losses associated with our slow-light waveguides remain large, and we are addressing this problem both by developing improved fabrication methods and by developing designs that are relatively insensitive to the waveguide loss.

We are also working on the use of plasmonic devices in photonics. We are especially interested in developing devices based on the use of surface plasmon polaritons (SPPs), structures that confine light along metal-dielectric interfaces in regions much smaller than that light’s wavelength. This tight confinement can allow a tight packing of photonic devices in a small footprint, a key feature of highly integrated photonic circuits currently under development. Also, because metals are highly nonlinear and the light is tightly confined, SPPs produce a large nonlinear phase shift per unit length of propagation. Unfortunately, SPPs tend to show high loss, but University of Ottawa colleague and collaborator Pierre Berini has developed means for dramatically increasing the propagation distance of SPPs. Our joint research will consider the technical challenges surrounding the design of plasmonic amplifiers, lasers, modulators, and detectors, which could be used for telecommunications as well in more exotic settings, such as biochemical sensors that report on the chirality of organic molecules. The nonlinear photonic interactions driving these devices would open up the possibility of much more efficient nanoscale switching structures, which could become a staple item in the next generation of information technology and communications infrastructure.

Quantum mechanics has opened up various possibilities for the packaging and processing of information in ways that far exceed what was possible only a few years ago using “classical” methods. One of the most highly developed of these methods is secure communication based on quantum key distribution (QKD). The idea here is for data to be encoded using a traditional key or “one-time pad.” Quantum mechanical procedures are then used to transmit this key from the sender to the receiver. These quantum procedures ensure that if an eavesdropper intercepts this message, the quantum features of the transmitted photons will be modified in a manner that can easily be discerned by the receiver. The original demonstration of QKD made use of the polarization of light to encode information onto an individual photon, and thus each photon could carry only one bit of information. In contrast, we are developing a system in which we encode information onto individual photons using the orbital angular momentum (OAM) states of light. Because there is no limit to how much OAM a single photon can carry, there is in principle no limit to how much information can be carried by an individual photon in a QKD system. Our immediate goal is to impress as many as eight bits of information on a photon. We are doing this by diffracting individual photons from a computer-generated hologram written onto a spatial light modulator. We are also studying the impact that atmospheric turbulence could have on the propagation of these photons, which could lead to a degradation of the information content.

In support of our work in quantum technologies including secure optical communications, we are undertaking an extensive study of some of the fundamental aspects of quantum photonics. Topics currently under investigation include the development of laboratory measures to quantify the degree of entanglement between two optical fields and their mutual information content, the use of entanglement witnesses to perform such studies in an efficient manner, the use of quantum tomography to characterize quantum states, and techniques for the direct measurement of the quantum wavefunction. We are also very interested in developing methods for improved metrology based on the use of entangled photons and other quantum states of light.